The Problem |
Ordinary FIR filter design tools deliver a set of high precision filter coefficients meeting the filter requirements. |
|
|
|
FIR filters are often implemented using finite word length multipliers and adders, and therefore the high precision coefficients need to be rounded off somehow. This rounding process introduces errors to the filter and the quantized filter may not meet the filter requirements any more. |
|||
Ordinary Rounding |
Normally the rounding is performed using a conventional "round to nearest" approach resulting in a frequency domain error that is spread out over the entire frequency range. |
|
|
|
You can play around with the gain to get different rounding results but the magnitude of the error is typically not improving much. The solution often used is to increase the number of bits in the multipliers and adders until the filter requirements are met. |
|||
Noise Shaping |
If certain frequency bands are more critical than others, there is a way to control the effects of quantization in the frequency domain. A technique known as "noise shaping" is applied to data on a regular basis in A/D and D/A converters. Running at very high sampling frequencies (over sampling) D/A converters need only one bit to represent the low frequency signal components with very high accuracy. Analog low-pass filters outside the D/A converter takes care of the unwanted noise at higher frequencies. |
||
The Idea |
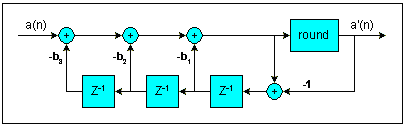
My idea is to apply a similar technique, but this time with the filter coefficients as input to the noise shaper. The following figure shows how high precision filter coefficients, a(n), are converted to fixed word length coefficients, a'(n), using a simple error feedback mechanism. The "round" function performs a simple "round to nearest" operation.
Figure 1. Noise shaping the filter coefficients. The multipliers (b1,b2,b3) control the noise shaping frequency characteristic. |
||
Choosing the multipliers |
We use b1= b2 =1.96285 and b3 = 1. The result is a low pass filter rejecting quantization noise in the high end of the frequency range. |
||
Delay line set-up |
Before we start feeding any filter coefficients to the noise shaper we need to initialize the three values of the delay line. This is done using a random generator with a uniform and uncorrelated output between -0.5 and 0.5. |
||
Finding a solution |
Now we feed the filter coefficients to the noise shaper starting with the center coefficient and going out to the tails. The set of quantized filter coefficients is analyzed using e.g. FFT. If it does not meet the filter requirements then the procedure is repeated with a new set of random delay line values. |
||
Does it work? |
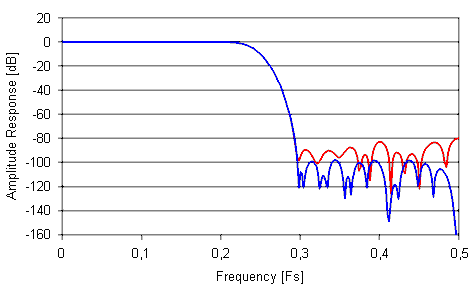
Within just 100 trials this method is likely to find a set of coefficients that improve the stop band damping by as much as 20 dB corresponding to a 3 bit reduction in multiplier word length. In this example the high precision filter has 69 coefficients. They are quantized using ordinary rounding and the new method. The result is shown in Figure 2 below. Click here to see the actual filter coefficients from this example. |
||
|
Figure 2. Results from ordinary rounding (red) and new method (blue) The amplitude response of the filter generated with ordinary rounding (red graph) has a maximum stop band ripple of -79.7 dB. The filter generated with the new method (blue graph) has an 18 dB improved stop band rejection. |
|||
IEEE Paper |
If you would like to take a look at the theory behind this technique you should check out this paper. It was published in the July 1989 issue of IEEE Acoustics Speech and Signal Processing (ASSP) : IEEE Paper. |
||
Software |
Mathworks has implemented the algorithm, read more about their Matlab solution here: I also found a link to this implementation: I would like to point to any software that implements this technique. Please let me know if you found or (even better) wrote such software |
||