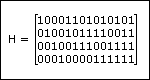Whats that? |
Error correcting codes is an example of deep mathematical theory used everyday by almost everyone: in mobile phones, DVDs, computer memory etc. Their use ensure high quality information even if the mobile link is bad, the DVD is scratched or the computer is running hot The QR ”bar code” uses the Reed-Solomon code to make the pattern robust to errors introduced by scratches and dirt. Try your QR scanner on these - they both work: |
|||
|
|
|
|
||
|
The basic idea is that first we add a relatively small amount of extra information to the data. Then at a later stage or in another place we get a copy of the data unfortunately with some unwanted changes added to it. Our solution detects these changes and recovers the disrupted data. Read more about error correcting codes on Wikipedia
|
||||
|
Youtube |
Visit my Youtube channel “Math Crumbs” to learn more about error correcting codes and how they work: |
|
||
C Source Code |
I’ve implemented a number of error correcting codes in C and would like make them available to other software developers. |
|||
|
The Hamming(15,11) and the Golay(23,12) implementations are available for free, even for commercial use. The Reed-Solomon implementation is free to download and non-commercial use is free. Commercial use is available for a small fee. Please read the conditions in the source file for further details. |
|
|||
|
|
|
|||
Hamming-Golay Source |
The encoder and decoder function for the Hamming and Golay codes. Includes a small demo program. |
|||
|
|
|
|
||
Hamming(15,11) |
A perfect binary code with 11-bit data input and |
|
||
Golay(23,12) |
A perfect binary code with 12-bit data input and 23-bit code words. Capable of correcting all single, double and triple bit error patterns. |
|||
Reed-Solomon Source |
The encoder and decoder function for the |
|||
Reed-Solomon
|
A byte-oriented code with (255-k)-byte data input and 255-byte code words. The number of parity bytes k determines the error correcting capability. The decoder handles errors and erasures. An erasure is an error where the position, but not the value, is known. The decoder corrects all byte error/erasure patterns bounded by: (2*errorCount + erasureCount) <= k |
|||
Questions |
If you have any questions please don’t hesitate to contact me. There is no FAQ available at the moment. |
|||
|
|
|
|
|
|